混相流解析
混相流とは
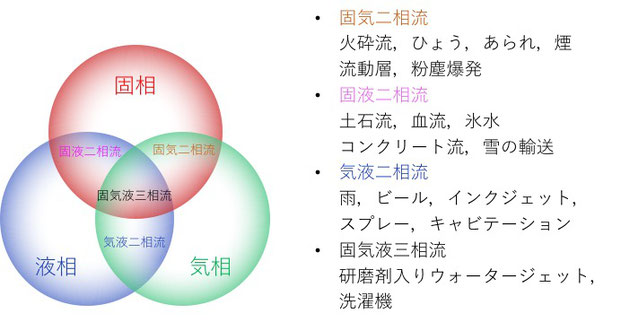
混相流の分類と混相流現象の例
物質の状態には固体、液体、気体の3つの状態(相)があり、気体または液体だけの流れを単相流(Singlephase flow)、複数の相が混在している流れのことを混相流(Multiphase flow)といいます。混相流は上図に示されているように大きく分けて4つに分類することができます。混相流現象の例を見て分かる通り、雨や霧など身のまわりで見られる自然現象や洗濯機やスプレーなどの工業製品においても混相流現象を見ることができます。
このように混相流現象は様々なところで起きるため、現象の基礎的な理解というものが産業分野や防災分野など幅広い分野から求められており、実験やシミュレーションによって現象を理解する試みが数多くなされています。
松尾研究室では、急激な燃焼を伴う粉塵爆発や高速で水中を移動する飛翔体周りのキャビテーションなど流体の圧縮性を考慮した混相流現象に重点を置き、数値シミュレーションを用いた固気二相流および気液二相流の解析を行っております。
固気二相流解析
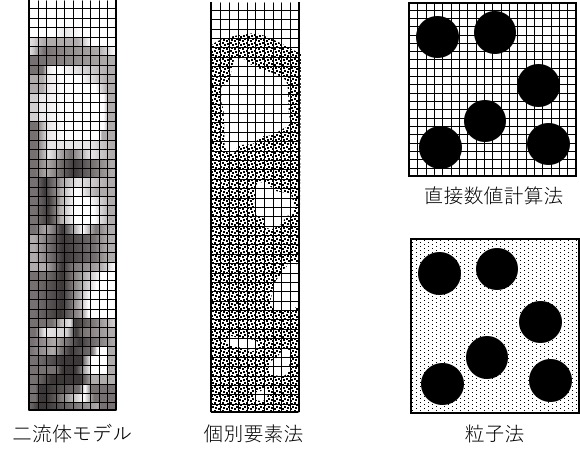
固気二相流における数値計算手法の例
数値計算手法には大きく分けて2つの手法があります。一つは相を連続体として考え、計算格子を用いてNavier-Stokesの式を解くEulerian手法で、もう一つは相を粒子の集まりと考え、個々の粒子をLagrange的に追跡することによって流れ場を解くLagrangian手法です。固気二相流解析においては気相および固相に対してそれぞれどの手法を用いるかの組み合わせによって数多くの手法が存在します。その一例をいくつか説明します。
・ 二流体モデル(Eulerian-Eulerian)
二流体モデルは流体である気相だけでなく固相に関しても連続体として扱い、各相とも流体の考えに基づいてNavier-Stokes型の方程式が基礎方程式として用いられます。二流体モデルの利点としては粒子の挙動を平均化して流体としてみなすことから計算負荷が小さいことが挙げられます。しかしながら、粒子の挙動を平均化していることから個々の粒子の離散的な動きを詳細に解析することができないといった欠点があります。
・ 個別要素法(Eulerian-Lagrangian)
個別要素法は固相を格子よりも小さな粒子の集まりと考え、粒子同士の衝突を直接再現する手法です。粒子間の衝突または反発現象の扱い方には粒子の変形がないと考える剛体球モデルと粒子の変形を考慮する軟体球モデルの2種類があります。個別要素法では固相を個々の粒子の集まりとして考えるため、粒子の離散的な動きを再現できる利点がありますが、計算負荷の点から扱える粒子数に制限があるといった欠点があります。
・ 直接数値計算法(Eulerian-Lagrangian)
直接数値計算法は格子の大きさは粒子の大きさよりも小さく、気相を連続体、固相を個々の粒子の集まりとして考える手法です。格子が粒子よりも小さいため粒子表面の局所的な固気相間の相間作用を算出できるという利点があります。しかしながら、求められる格子点数が多くなるため計算負荷が大きくなるといった欠点があります。
・ 粒子法(Lagrangian-Lagrangian)
粒子法は固相を粒子の集まりとしてみなし、気相に関しても粒子(気体原子、分子)の集まりとみなして流れ場を解く手法です。気相も粒子の集まりとみなしていることからより原理的には優れた解析手法と言えますが、扱う粒子数が他の計算手法と比較して膨大な数になることから計算負荷の点で0.001 m以下のスケールでの解析が主となるといった問題があります。
このように固気二相流解析においても数多くの計算手法が存在し、解析対象やどのような現象に注目するかによって計算手法の選択を行います。
混相流の本質は各相が相互に影響し合うことにあり、これを相間作用といいます。
相間作用は大きく分けて次の3つに分類されます。
相間作用の分類
・ 質量の移動
ー 蒸発,燃焼 など
・ 運動量の移動
ー 流体抵抗力,揚力 など
・ エネルギーの移動
ー 対流熱伝達 など
固気二相流の場合では相間作用は粒子表面で生じるため、相間作用を算出する方法としては粒子表面の流れをNavier-Stokesの式を用いて解き、その結果から粒子表面の局所的な相間作用を表面全体にわたって積分して求める方法が原理的に優れていると言われています。しかしながら、計算負荷の面で個々の粒子に対してこの算出方法を用いるのは困難なことから、相間作用の算出にはある条件下で得られた理論式や経験式を適用する方法が主に用いられています。
理論式や経験式などは数多くありそれぞれ適用できる条件が異なるため、解析で用いる上では適切な理論式、経験式を用いる必要がありどの式を適用すべきかの研究も数多くされています。
3.気液二相流解析
気液二相流とは,気相と液相が混在した流れであり,水と水蒸気のように同じ物質の二つの相が共存した流れを一成分二相流と呼び,水と空気のように異なる物質が混在した流れを二成分二相流と呼びます.
気液二相流においては,気相と液相の界面が様々な幾何学的形状を呈し,それが時間的に変化するために流れの様相(流動様式)は複雑です.しかも,両相は界面を通じて相互作用するために,流れの特性は界面の形状や分布に大きく依存します.気液二相流の代表的な流動様式を下図に示します.ここでは,各相の分布が連続か不連続かによって流動様式を分類しています.

気液二相流の流動様式
気液界面の変形や,物質の融解・凝固などの物理現象により界面の形状が決定される問題は自由境界問題と言われています.自由境界問題の難しさは,界面の形状が支配方程式より与えられる解の一部として得られるため,数学的定式化及び数値安定性などに困難を伴うことです.自由境界の計算手法は,以下の三つの方法に大別されます.
・オイラー法:空間に固定された格子内を移動する界面に関して,界面を表す関数を移流することにより界面の移動を表現する方法です.界面を表す関数には,VOF法,Level Set法,Diffuse interface Mode法などがあります.このように界面の移動を,界面と関連付けて定義される関数の値の変化から追跡する方法を界面捕獲法とも呼びます.
・ラグランジェ法:界面上に存在する流体粒子の移動を直接追跡し,界面の移動を計算する方法です.代表的なものにMAC法があります.このように界面を陽に表現する方法を界面追跡法とも呼びます.
・ALE法:オイラー法とラグランジェ法の混合型の方法です.界面の追跡をラグランジェ的に行った場合,移動後の界面要素の形状が大きく歪んだり,要素の空間分布に疎密が生じ,数値的安定性や計算精度に問題を生じることがあります.ALE法では,ラグランジェ的に移動した格子点について,各点を結ぶ3次スプラインを形成し,その3次スプライン上で格子点を適切な位置に移動することにより再配置を行います.
<参考文献>
日本混相流学会,’混相流ハンドブック’,朝倉書店,2004
M.A. van der Hoef et al., Numerical Simulation of Dense Gas-Solid Fluidized Beds: A Multiscale Modeling Strategy, Annual Review of Fluid Mechanics, 2008
日本機械学会,’改訂 気液二相流技術ハンドブック’,コロナ社,2006
高木周,’マイクロ分散相流れの基礎と応用’,http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/110790/1/KJ00004579927.pdf
